Prime Calc Apk 0.6

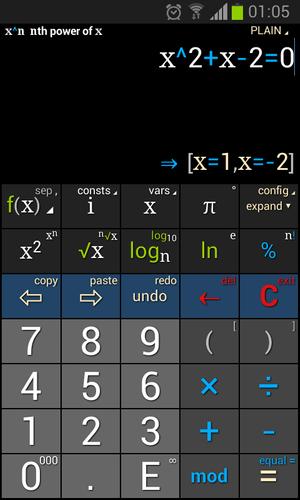
강력한 과학 계산기, 연기, 매트릭스, 적분 및 파생 상품

PRIMECALC- 자유 과학적 상징적 계산기

-70 개의 기능, 20 개의 수학 상수 및 최대 6 개의 변수

- 새로운 기능과 상수는 사용자가 정의 할 수 있습니다.

- 복소수를 지원합니다

- 매트릭스, 벡터, 세트 및 계산

- 수학적 방정식을 해결합니다

- 적분 및 파생 상품을 계산합니다

-단계별 계산

- 그리고 더 많은

지원되는 기능, 연산자 및 수학 상수 :

산수:

연산자 +, -, ×, ÷, %

x^n- x의 전력

√ (x) - x의 제곱근

√ (n, x) - x의 n 번째 루트

ln (x) - x의 자연 로그

log (x) - x의 로그에서베이스 10

log (n, x) - x에서 base n의 로그

장

짐

수학적 분석 :

∫ (f (x)) - f (x)의 무기한 적분

짐

∂ (f (x)) - f (x)의 미분

lim (f (x), c) - x에 접근 할 때 f (x)의 한계 c

방정식 해결 :

다항식의 표현 -x^2+3x -2 = 0

= - 다항식 방정식 연산자

수치 기능 :

m 모드 n- 나머지 m ÷ n

GCD (M, N) - M 및 N의 가장 큰 일반적인 제수

LCM (M, N) - 최소한의 M 및 N

ABS (N) - N의 절대 값

라운드 (n) - n에 가장 가까운 정수

frac (n) - n의 분수 부분

바닥 (n) - n의 바닥 값

CEIL (N) - N의 천장 값

복소수 :

표현 -5+2I

Re (c) - 복소수의 실제 부분 c

IM (C) - 복소수의 가상 부분 c

통계:

중앙값 ([a]) - [a]의 중앙값

gmean ([a]) - [a]의 기하학적 평균

Amean ([a]) - [a]의 산술 평균

randi (n) - 0에서 n까지의 랜덤 정수

randr- 랜덤 레알 0에서 1까지

숫자 이론 :

고조파 (N) - Nth 고조파 번호

조합 :

N! - n의 factorial

이항 (n, k) - 이항 계수

다국적 (N1, N2, ...) - 다중 생물 계수

Catalann (N) - Nth 카탈로니아어 번호

fibonacci (n) - nth fibonacci 번호

삼각법 :

sin (x), cos (x), tan (x)

SEC (X), CSC (X), COT (X)

asin (x), acos (x), atan (x), acot (x)

쌍곡선 기능 :

sinh (x), cosh (x), tanh (x)

arsinh (x), Arcosh (x), artanh (x)

매트릭스 :

표현 - [[1,2], [3,4]]

[M1] ⋅ [M2] - [M1] 및 [M2]의 제품

tran ([m]) - 전환 [m]

ctran ([m]) - 컨쥬 게이트 및 전환 [M]

역 ([m]) - 반전 [m]

det ([m]) - [m]의 결정 요인

tr ([m]) - [m]의 흔적

mpow ([m], n) - [m]의 nth 행렬 전력

번호 세트 :

표현 - [1,2]

Union ([A1], [A2]) - 두 세트의 연합

Intersec ([a1], [a2]) - 두 세트의 교차점

max ([a]) - [a]의 가장 큰 요소

최소 ([A]) - [A]의 가장 작은 요소

상수 :

π- 숫자 pi

E -Euler의 번호

I- 상상의 단위

∞ - 무한대

γ -Euler – Mascheroni 상수

G- 카탈로니아의 상수

A- 글레이 쉬 - 킨 켈린 상수

φ- 황금 비율

κ- 킨친의 상수

C₂- 트윈 프라임 상수

하거나 Apéry의 상수

B₄- Brun 's Constant for Prime Ququplets

B₂- Brun 's Constant for Twin Primes

eb -erd–s – orborwein constant

δ- Feigenbaum 첫 번째 상수

α- Feigenbaum 두 번째 상수

BL- Legendre 's Constant

m ₁ - Meissel – Mertens가 일정합니다

최신 버전의 새로운 기능 0.6